HMO法計算－Butadieneの解答

Hückel分子軌道法計算

原子数に対応した次数の対角要素が0の対角行列を作成します。
結合に相当する行列要素の値を１に置き換えます。
固有値と固有ベクトルを求めます。

Butadiene

$DiagonalMatrix[{0, 0, 0, 0}]//MatrixForm$

$(\[NoBreak] 0 0 0 0 \[NoBreak]) 0 0 0 0 0 0 0 0 0 0 0 0$

$(\[NoBreak] 0 1 0 0 \[NoBreak]) 1 0 1 0 0 1 0 1 0 0 1 0$

$Eigensystem[(\[NoBreak] 0 1 0 0 \[NoBreak])]//N 1 0 1 0 0 1 0 1 0 0 1 0$

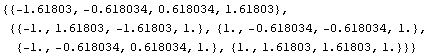
${{-1.61803, -0.618034, 0.618034, 1.61803}, {{-1., 1.61803, -1.61803, 1.}, {1., -0.618034, -0.618034, 1.}, {-1., -0.618034, 0.618034, 1.}, {1., 1.61803, 1.61803, 1.}}}$

$E_1$ =  α + 1.618β       $\[CurlyPhi]_1 = c_1 (φ_1$ + 1.618 $φ_2$ + 1.618 $φ_3 + φ_4$ )
$E_2$ =  α + 0.618β       $\[CurlyPhi]_2 = c_2 (φ_1$   + 0.618 $φ_2$ - 0.618 $φ_3 - φ_4$ )
$E_3$ =  α  - 0.618β      $\[CurlyPhi]_3 = c_3 (φ_1$ - $0.618 φ_2 - 0.618 φ_3 + φ_4)$ )
$E_1$ =  α - 1.618β       $\[CurlyPhi]_4 = c_4 (φ_1$ - 1.618 $φ_2$ + 1.618 $φ_3 - φ_4$ )

　と求められました。

　分子軌道の係数を規格化すると

　 $E_1$ =  α + 1.618β    　
　 $E_2$ =  α + 0.618β
　 $E_3$ =  α  - 0.618β
　 =  α - 1.618β

　となります。

戻る